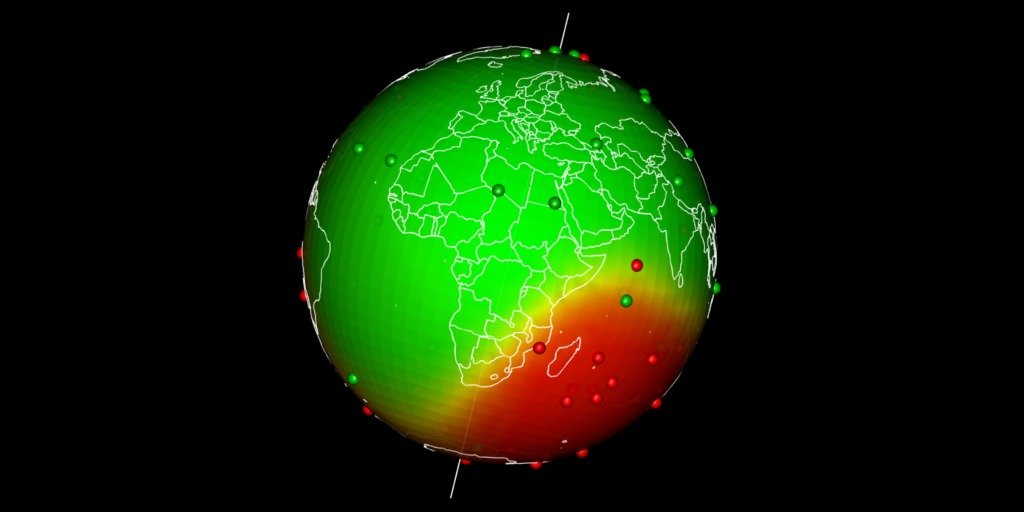
Interpolation spatiale à l’échelle de la Terre
La carte de la Terre est habituellement présentée à plat. Les coordonnées géographiques vont généralement de -180° à +180°. Les interpolations spatiales qui utilisent directement les coordonnées géographiques peuvent être compliquées car -180° est égal à +180°. Je propose ici une façon de réaliser des interpolations spatiales sur le globe terrestre en tant que sphère puis de cartographier les sorties en 3D avec rgl.
Jeu de données aléatoire
Créons un jeu de données aléatoires avec des observations de présences et d’absences sur le globe (Ce qui est simulé avec un peu d’auto-corrélation spatiale Nord / Sud). Nous ne tenons pas compte de la différence possible entre les zones terrestres et océaniques.
J’utilise une astuce ‘modulo’ pour limiter les coordonnées entre -180° et +180°. C’est juste pour garder une trace de cette astuce (sinon j’aurais pu utiliser runif pour simuler des données).
# library(sp)
library(rgdal)
library(sf)
library(raster)
library(ggplot2)
# Simulate dataset with a little spatial auto-correlation
set.seed(42)
n <- 30
obs <- rbind(data.frame(lon = rnorm(n, 0, 180),
lat = rnorm(n, 50, 35),
value = 0),
data.frame(lon = rnorm(n, 180, 180),
lat = rnorm(n, -50, 35),
value = 1))
# Modulo trick
obs$lon <- obs$lon %% 360 -180
obs$lat <- obs$lat %% 180 -90
# Transform points as spatial points with sf ----
obs_sf <- st_as_sf(obs, coords = c("lon", "lat"),
crs = 4326)
# Plot on a worldmap
worldmap <- borders("world",
colour = "#fefefe",
fill = "#808080"
)
# Plot over a worldmap
ggplot() + worldmap +
geom_point(data = obs,
aes(x = lon, y = lat,
colour = factor(value))) +
coord_quickmap()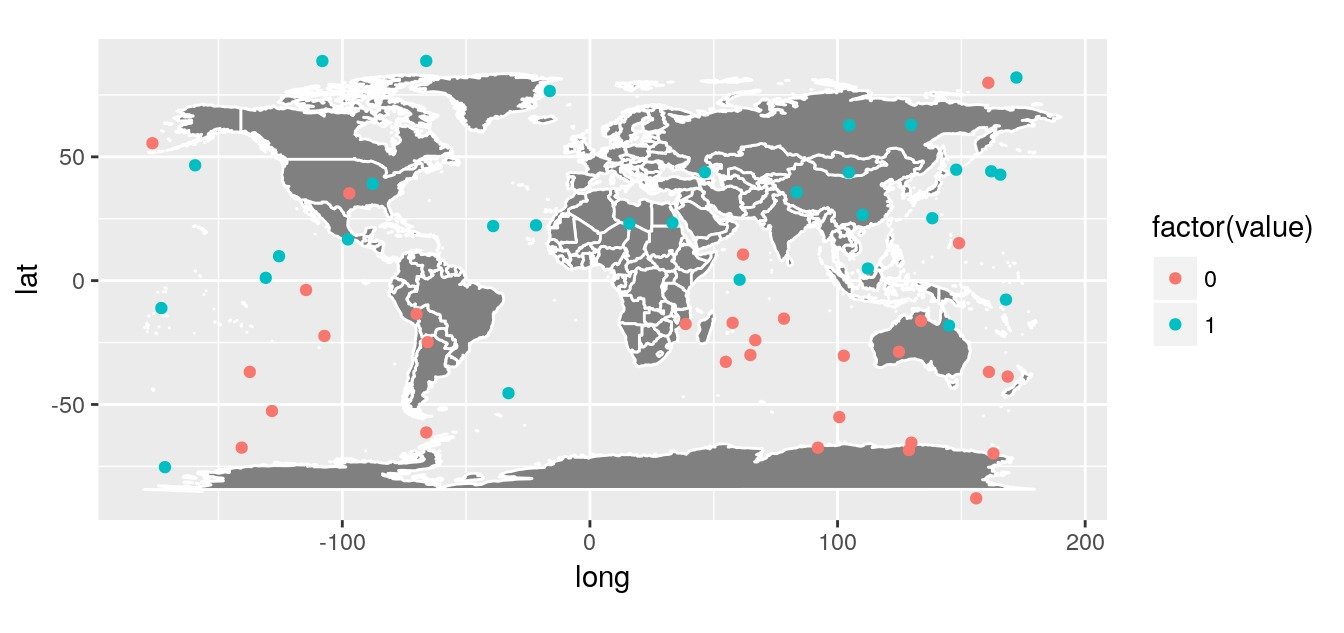
Interpolation par distance inverse
Une interpolation simple est l’interpolation par l’inverse de la distance. Nous pouvons calculer les distances entre les observations et la carte du monde en utilisant le ‘Great Circle’.
- Créez une
rastervide qui sera utilisé pour les interpolations. - Transformer les observations en points spatiaux avec la bibliothèque
sf. - Calculer les distances (‘great circle’) entre les points et les cellules du raster
- Interpoler en utilisant l’interpolation avec distance inverse
# Create an empty world raster ----
ny <- 41
nx <- 80
r <- raster(
nrows = ny, ncols = nx,
crs = '+proj=longlat',
xmn = -180, xmx = 180,
ymn = -90, ymx = 90
)
# Transform raster as spatial points with sf
r_sf <- st_as_sf(as.data.frame(coordinates(r)),
coords = c("x", "y"),
crs = 4326)
# Distance between points and raster ----
obs.r.dists <- st_distance(obs_sf, r_sf)
obs.r.dists <- unclass(obs.r.dists)
# Inverse distance interpolation ----
## pred = 1/dist^idp
idp <- 2
inv.w <- (1/(obs.r.dists^idp))
z <- (t(inv.w) %*% matrix(obs$value)) / apply(inv.w, 2, sum)
# Fill in raster for predictions
r.pred <- r
values(r.pred) <- z
# Plot prediction raster
worldmap_predict <- borders("world",
colour = "#05050541",
fill = NA,
size = 0.5
)
rasterVis::gplot(r.pred) +
geom_tile(aes(fill = value)) +
scale_fill_gradient2(low = 'red', mid = "yellow",
high = 'green', midpoint = 0.5) +
geom_point(data = obs,
aes(x = lon, y = lat, colour = factor(value))) +
worldmap_predict +
guides(colour = FALSE) +
coord_quickmap()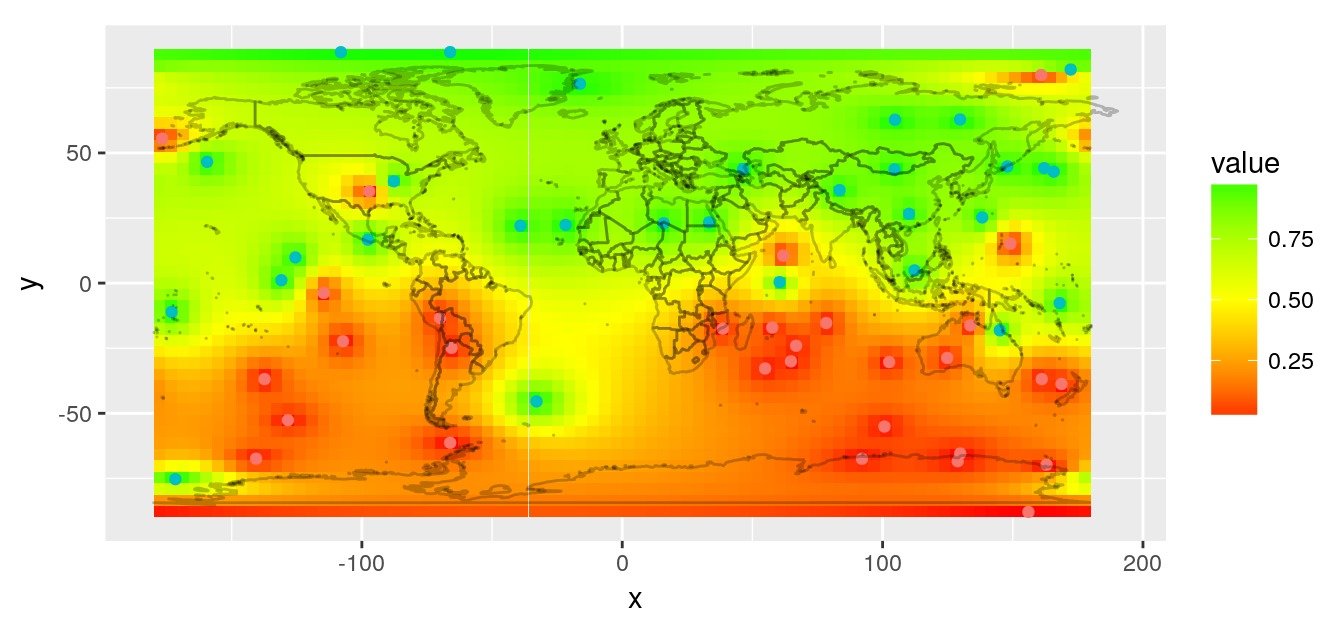
Krigeage avec distances définies par l’utilisateur
Pour interpoler le jeu de données, vous pouvez utiliser le krigeage. Cette interpolation s’appuie sur un variogramme permettant d’utiliser la structure spatiale des données (contrairement à “idw” qui est fixé par l’utilisateur).
Pour les interpolations avec des distances et des obstacles personnalisés, j’ai créé la librarie (totalement en développement) GeoDist. Ici, nous n’avons pas d’obstacles, mais nous avons une matrice de distances définie par l’utilisateur basée sur le ‘Great Circle’ que nous voulons utiliser pour adapter un variogramme et interpoler sur la carte. Dans GeoDist, j’ai modifié certaines fonctions de la librairie geoR pour pouvoir calculer un variogramme et interpoler en utilisant une matrice de distances définie par l’utilisateur.
Calculons le variogramme en fonction de notre propre matrice de distances avec GeoDist::variog.dist.
library(GeoDist)
# Transform data as geodata for geoR library
datageo <- as.geodata(obs, data.col = "value")
# Calculate distances between observations
obs.obs.dists <- st_distance(obs_sf)
obs.obs.dists <- unclass(obs.obs.dists)
# Create variogram with custom distances
data.v <- variog.dist(
datageo,
trend = "cte",
dist.mat = obs.obs.dists,
max.dist = max(obs.obs.dists),
breaks = seq(0, max(obs.obs.dists), length.out = 10))
# Fit variogram
data.vfit <- geoR::variofit(
data.v,
cov.model = "exponential")
# Plot
plot(data.v); lines(data.vfit, col = "blue")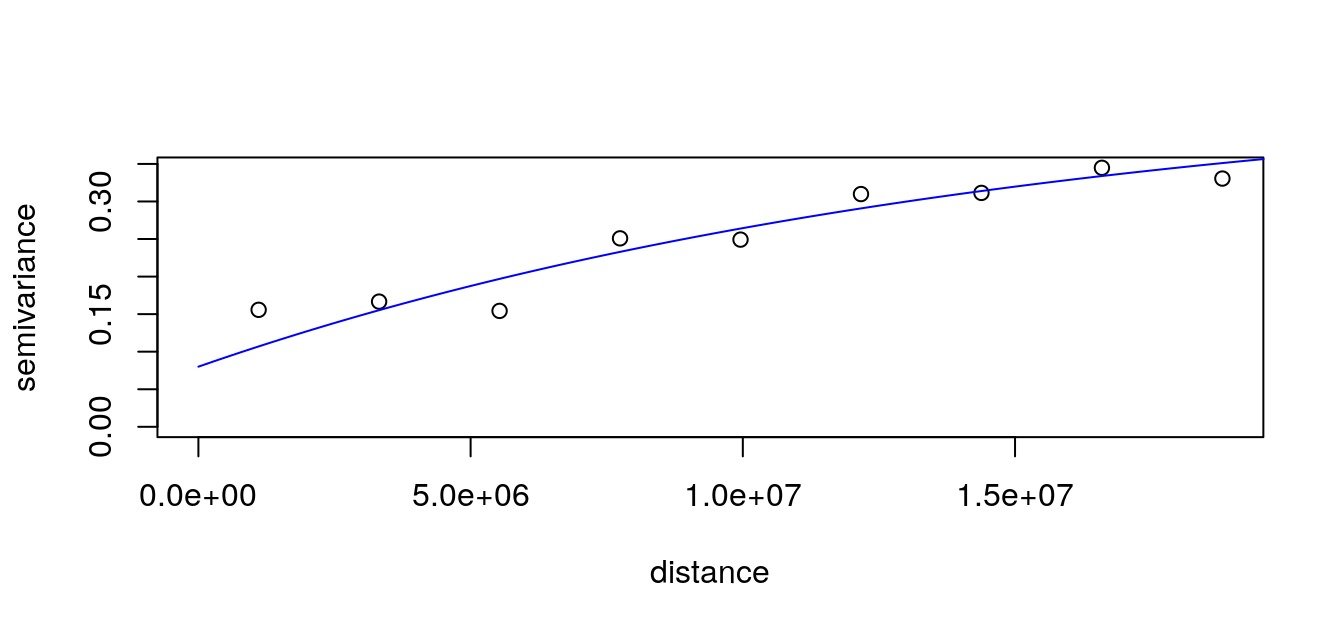
Nous utilisons le variogramme pour prédire sur toute la carte, en utilisant également des distances personnalisées avec GeoDist::krige.conv.dist.
# Distances to raster
obs.r.dists <- st_distance(obs_sf, r_sf)
obs.r.dists <- unclass(obs.r.dists)
# Distances between raster locations
r.r.dists <- st_distance(r_sf, r_sf)
r.r.dists <- unclass(r.r.dists)
# Krige with custom distances
r.krige <- krige.conv.dist(
geodata = datageo,
locations = coordinates(r),
krige = krige.control(obj.model = data.vfit),
dist.mat = obs.obs.dists,
loc.dist = obs.r.dists,
loc.loc.dist = r.r.dists)
# Fill in raster with predictions
r.pred <- r
values(r.pred) <- r.krige$predict
# Plot prediction raster
rasterVis::gplot(r.pred) +
geom_tile(aes(fill = value)) +
scale_fill_gradient2(low = 'red', mid = "yellow",
high = 'green', midpoint = 0.5) +
geom_point(data = obs,
aes(x = lon, y = lat, colour = factor(value))) +
worldmap_predict +
guides(colour = FALSE) +
coord_quickmap()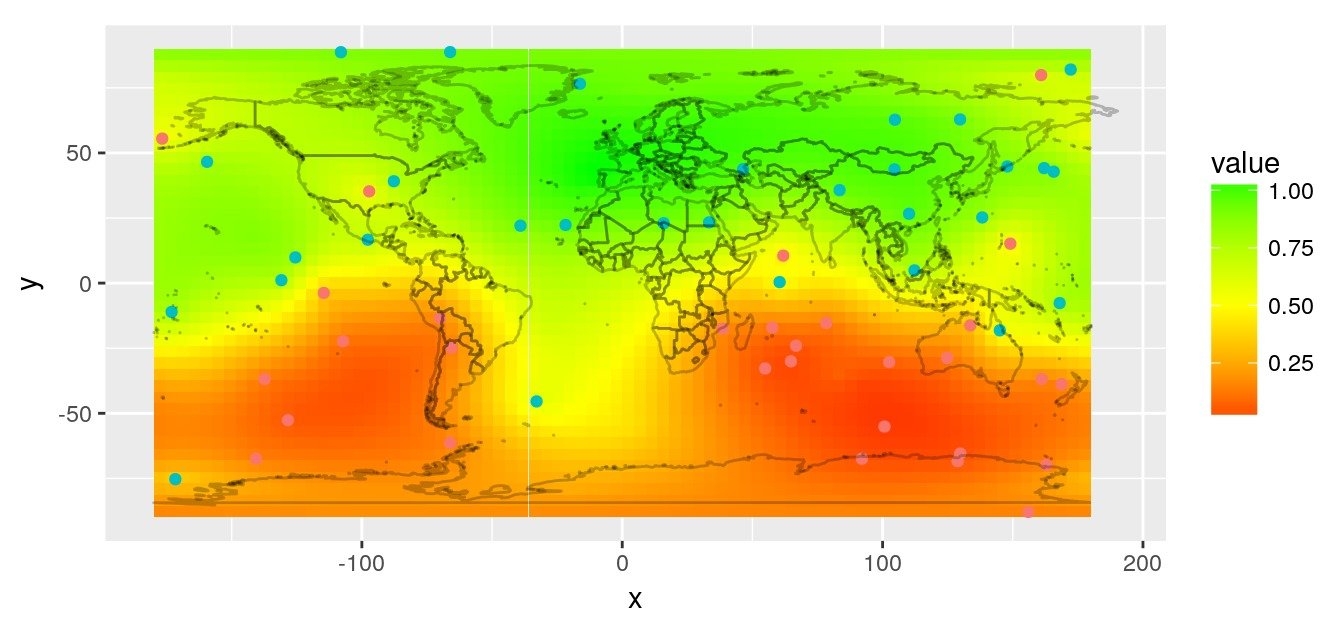
Ajuster un modèle gam sur des coordonnées 3D
Si vous voulez modéliser la distribution globale, avec un GAM par exemple, en utilisant la latitude et la longitude, vous ferez face à la discontinuité dans les coordonnées de longitude. Dans ce cas, il peut être préférable d’utiliser les coordonnées 3D-cartésiennes. Dans GeoDist, j’ai inclus la fonction sph2car pour transformer les coordonnées géographiques en coordonnées cartésiennes. C’est une modification de sphereplot::sph2car qui permet d’inclure l’aplatissement de l’éllipsoïde (geosphere::refEllipsoids()).
# Transform data in 3D ----
library(ggplot2)
library(maptools)
library(raster)
library(rgl)
# Transform observation in cartesian coords
obs.cart <- data.frame(sph2car(obs[,1:2]), value = obs$value)
# Approximation with a gam model
library(mgcv)
gam1 <- gam(value ~ te(x, y, z, k = 3),
data = obs.cart,
family = binomial)
# Predict on Raster
r.cart <- data.frame(sph2car(coordinates(r)))
pred <- predict(gam1, r.cart, type = "response")
r.pred <- r
values(r.pred) <- c(pred)
# Plot prediction raster
rasterVis::gplot(r.pred) +
geom_tile(aes(fill = value)) +
scale_fill_gradient2(low = 'red', mid = "yellow",
high = 'green', midpoint = 0.5) +
geom_point(data = obs,
aes(x = lon, y = lat, colour = factor(value))) +
worldmap_predict +
guides(colour = FALSE) +
coord_quickmap()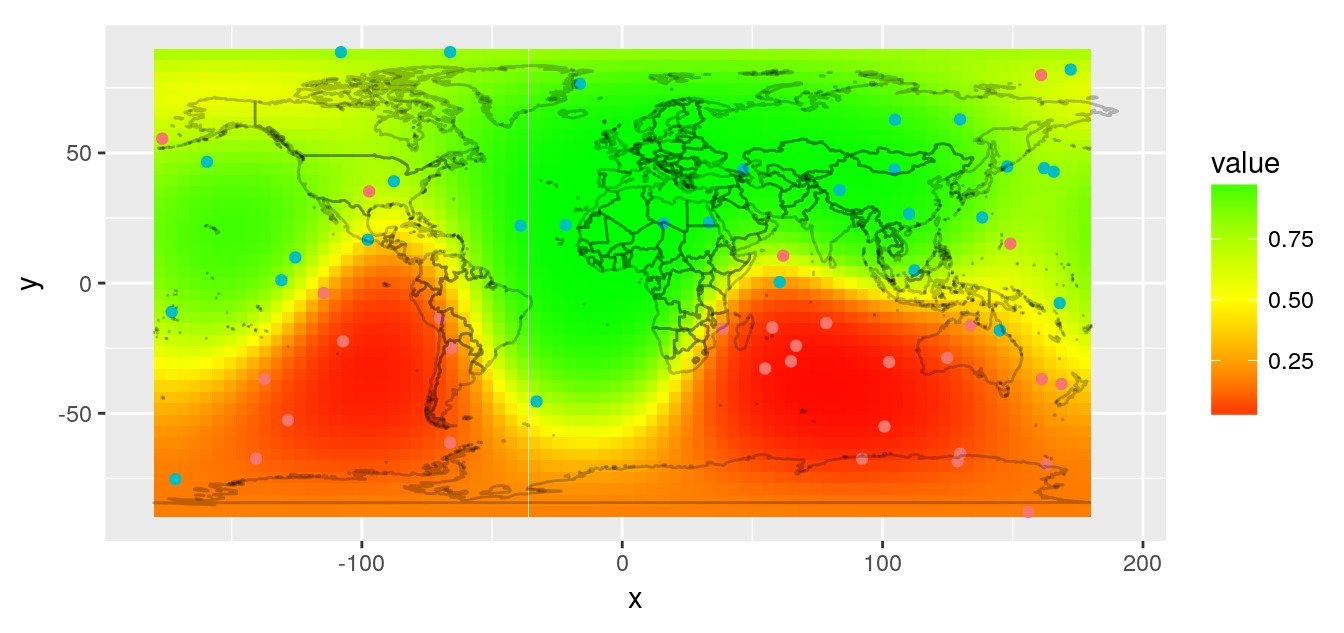
Tracer des prédictions sur un globe avec rgl
Il y a différentes façons d’obtenir une projection permettant d’afficher la Terre avec une forme de globe puis de créer une rotation en gif. Pour ma part, j’aime bien utiliser la librairie rgl parce que la sortie est interactive et je peux facilement voyager dans le monde en déplaçant ma souris.
La projection de notre carte de prédiction dans un graphique 3D de rgl nécessite quelques étapes:
- Construire la représentation 3D du raster de prédiction par triangulation
- [Edit: 2017-11-06] Créer une triangulation 3D directement avec
geometry::convhulln(Merci à @mdsumner) - [retiré] Trianguler les deux moitiés du globe séparément en utilisant la bibliothèque
deldir. - [retiré] Combiner les deux moitiés
- [Edit: 2017-11-06] Créer une triangulation 3D directement avec
- Créez des couleurs pour chaque facette triangulaire en fonction des prévisions
- Dessiner la carte 3D avec
rgl- Drapage du globe avec les prédictions avec
triangles3d. - Ajouter les observations en tant que
spheres3d. - Ajouter l’axe de rotation de la Terre pour le plaisir
- Drapage du globe avec les prédictions avec
- Ajouter une carte du monde sur la sphère 3d
- Récupérer les coordonnées géographiques et transformer en coordonnées cartésiennes avec la fonction
sph2car.
- Récupérer les coordonnées géographiques et transformer en coordonnées cartésiennes avec la fonction
- Utilisez les fonctions
transform3detrotationMatrixpour faire pivoter la Terre et récupérer les images de la rotation- Créer un gif
# Plot in 3d using rgl ----
library(geometry)
library(dplyr)
library(rgl)
# ---- Edit - 2017-11-06 ----
# Triangulate entire globe directly with geometry ----
# Thanks to Michael Sumner @mdsumner
tri3d <- geometry::convhulln(r.cart)
r.cart.tri <- r.cart[t(tri3d), ] %>%
mutate(n = c(t(tri3d)))
# Edit: Kept here as reminder but simpler with "geometry"
if (FALSE) {
# _With deldir = 2D triangulation ----
library(deldir)
# Triangulate top half of the globe
r.cart.top <- as.data.frame(r.cart) %>% as.tbl() %>%
mutate(n = 1:n()) %>%
filter(z >= 0)
r.cart.top.del <- deldir(as.data.frame(r.cart.top[,1:2]))
r.cart.top.tri <- do.call(rbind, triang.list(r.cart.top.del))
r.cart.top.tri$n <- r.cart.top$n[r.cart.top.tri$ptNum]
# Triangulate bottom half of the globe
r.cart.bottom <- as.data.frame(r.cart) %>% as.tbl() %>%
mutate(n = 1:n()) %>%
filter(z <= 0)
r.cart.bottom.del <- deldir(as.data.frame(r.cart.bottom[,1:2]))
r.cart.bottom.tri <- do.call(rbind, triang.list(r.cart.bottom.del))
r.cart.bottom.tri$n <- r.cart.bottom$n[r.cart.bottom.tri$ptNum]
# Combine top and bottom
r.cart.tri <- rbind(r.cart.top.tri, r.cart.bottom.tri) %>%
mutate(z = r.cart[.$n,"z"])
}
# ---- End of Edit ----
# Define a vector of colors for predictions
n.break <- 20
colors <- alpha(colorRampPalette(c("red", "yellow", "green"))(n.break), .4)
brk <- seq(0, 1, len = n.break + 1)
pred.col <- colors[as.numeric(as.character(
cut(pred, breaks = brk, include.lowest = TRUE, labels = 1:n.break)))]
# Print in 3d
triangles3d(r.cart.tri$x,
r.cart.tri$y,
r.cart.tri$z,
col = pred.col[r.cart.tri$n],
alpha = 0.9,
specular = "black")
# Observation with radius in scale of coordinates
spheres3d(obs.cart[,1:3],
radius = rep(0.2e6, nrow(obs.cart)),
color = obs.cart[,4] + 2)
# Black background
rgl.bg(color = c("black"))
# Add Earth rotation axe
segments3d(x = c(0,0),
y = c(0,0),
z = c(min(r.cart.tri$z)*1.2,
max(r.cart.tri$z)*1.2),
col = "white",
lwd = 2)
# Map world on the 3d sphere ----
library(rworldmap)
data(countriesCoarse)
for (i in 1:nrow(countriesCoarse)) { # i <- 1
Pols <- countriesCoarse@polygons[[i]]
for (j in 1:length(Pols)) { # j <- 1
lines3d(data.frame(sph2car(
countriesCoarse@polygons[[i]]@Polygons[[j]]@coords
)), col = "white", lwd = 2)
}
}
# Rotate and save as gif
# extraWD: directory where to save img of rotation
nb.img <- 45
angle.rad <- seq(0, 2*pi, length.out = nb.img)
# NorthPole on top, Europe-Africa in front.
uM0 <- rotationMatrix(-pi/2, 1, 0, 0) %>%
transform3d(rotationMatrix(-pi/2, 0, 0, 1)) %>%
transform3d(rotationMatrix(-pi/12, 1, 0, 0))
# Change viewpoint
rgl.viewpoint(theta = 0, phi = 0, fov = 0, zoom = 0.7,
userMatrix = uM0)
for (i in 1:nb.img) {
# Calculate matrix rotation
uMi <- transform3d(uM0, rotationMatrix(-angle.rad[i], 0, 0, 1))
# Change viewpoint
rgl.viewpoint(theta = 0, phi = 0, fov = 0, zoom = 0.7,
userMatrix = uMi)
# Save image
filename <- paste0(extraWD, "/gif/pic", formatC(i, digits = 1, flag = "0"), ".png")
rgl.snapshot(filename)
}
# Create gif
system(glue::glue("convert -delay 10 {extraWD}/gif/*.png -loop 0 ../../static{StaticImgWD}/Globe3D_rgl.gif"))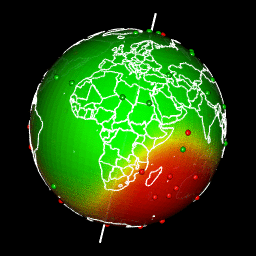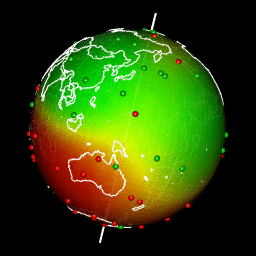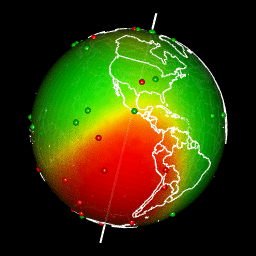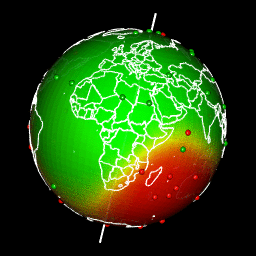
Citation :
Merci de citer ce travail avec :
Rochette Sébastien. (2017, nov.. 01). "Interpolation spatiale sur le globe terrestre 3D". Retrieved from https://statnmap.com/fr/2017-11-01-interpolation-spatiale-sur-le-globe-terrestre-3d/.
Citation BibTex :
@misc{Roche2017Inter,
author = {Rochette Sébastien},
title = {Interpolation spatiale sur le globe terrestre 3D},
url = {https://statnmap.com/fr/2017-11-01-interpolation-spatiale-sur-le-globe-terrestre-3d/},
year = {2017}
}